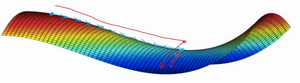
mini_batch
运行一整个数据集才能梯度下降一次太慢了 → 每mini-batch下降
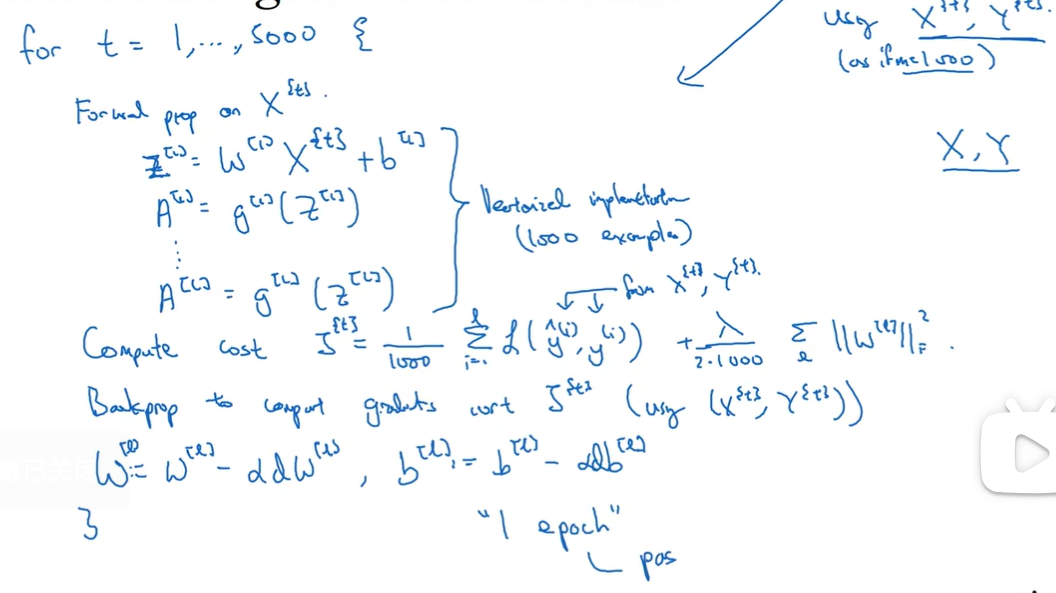 epoch 是迭代了一次数据集
epoch 是迭代了一次数据集
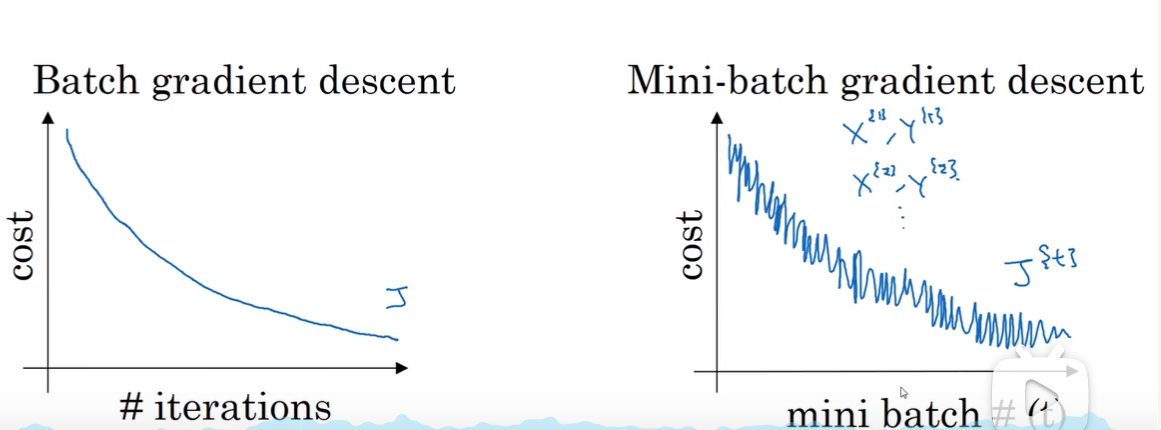
mini-batch大小:
- m 单次迭代耗时太长
- 1: SGD 每次一个样本:1)很多噪声(可以通过减小学习率改善)2)失去向量化的加速
- 1-m
指数加权移动平均
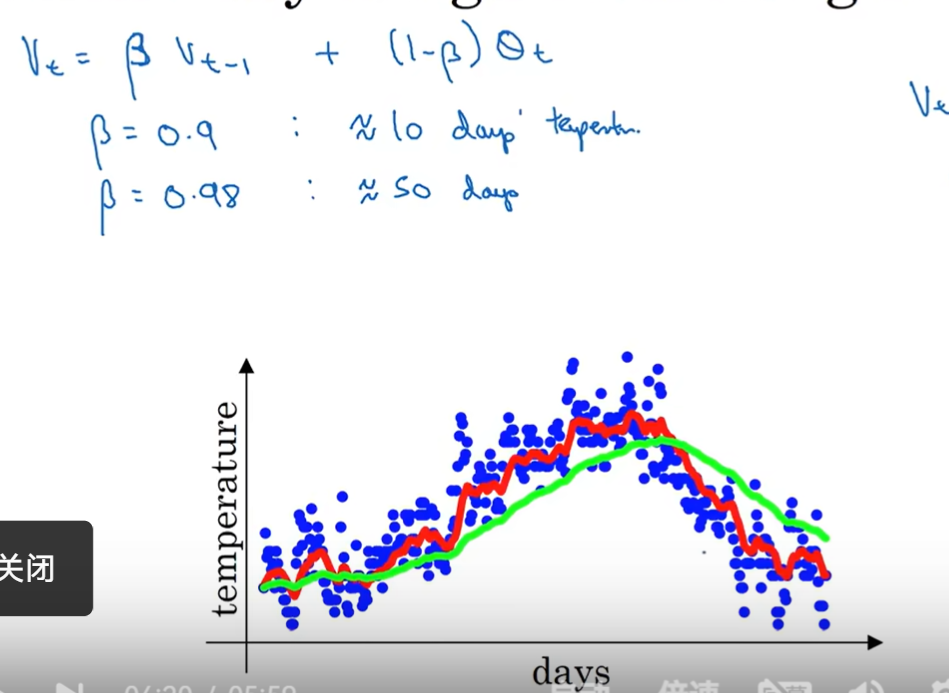
越大说明越多平均了前一天的温度 ,所以是更平缓(绿色)
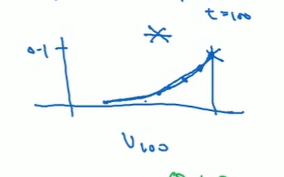 这个函数 作为 权重,乘上每天温度平均得到预测值。 相当于只关注了前十天的温度(因为10之前的权重过小)
这个函数 作为 权重,乘上每天温度平均得到预测值。 相当于只关注了前十天的温度(因为10之前的权重过小)
实际执行:
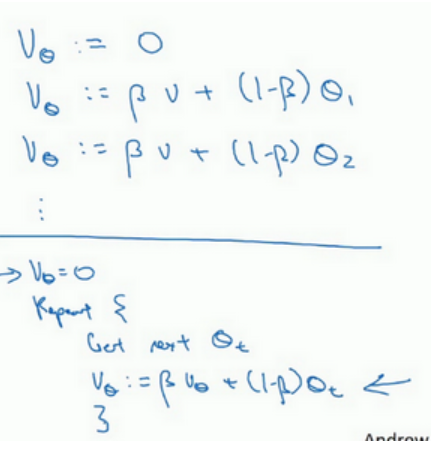
 指数加权平均数公式的好处之一在于,它占用极少内存,电脑内存中只占用一行数字而已,然后把最新数据代入公式,不断覆盖就可以了,正因为这个原因,其效率,它基本上只占用一行代码,计算指数加权平均数也只占用单行数字的存储和内存。
当然它并不是最好的,也不是最精准的计算平均数的方法。如果你要计算移动窗,你直接算出过去10天的总和,过去50天的总和,除以10和50就好,如此往往会得到更好的估测。但缺点是,如果保存所有最近的温度数据,和过去10天的总和,必须占用更多的内存,执行更加复杂,
指数加权平均数公式的好处之一在于,它占用极少内存,电脑内存中只占用一行数字而已,然后把最新数据代入公式,不断覆盖就可以了,正因为这个原因,其效率,它基本上只占用一行代码,计算指数加权平均数也只占用单行数字的存储和内存。
当然它并不是最好的,也不是最精准的计算平均数的方法。如果你要计算移动窗,你直接算出过去10天的总和,过去50天的总和,除以10和50就好,如此往往会得到更好的估测。但缺点是,如果保存所有最近的温度数据,和过去10天的总和,必须占用更多的内存,执行更加复杂,
偏差修正
初始阶段 对接下来有影响,修正为
Momentum:
 希望纵向减小摆动, 横向加速向前
计算梯度的指数加权平均
相当于加上动量,
实际中,在使用梯度下降法或动量梯度下降法时,人们不会受到偏差修正的困扰(因为 相当于平均10天的结果,10次迭代之后已经过了初始阶段)
希望纵向减小摆动, 横向加速向前
计算梯度的指数加权平均
相当于加上动量,
实际中,在使用梯度下降法或动量梯度下降法时,人们不会受到偏差修正的困扰(因为 相当于平均10天的结果,10次迭代之后已经过了初始阶段)

RMSprop(root mean square prop)
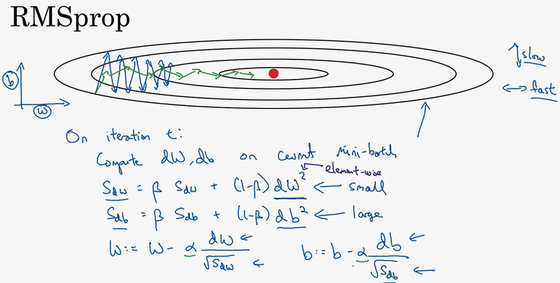
我们希望会相对较小,所以我们要除以一个较小的数,而希望又较大,所以下面更新的式子要除以较大的数字,这样就可以减缓纵轴上的变化 对于高维:最终去掉有摆动的方向 的平方根趋近于0?:作为分母,得到数非常大,为了保证稳定性,分母上加上一个很小的
Adam优化
RMPSprop与Adam 结合
 常用的缺省值为0.9
推荐使用0.999
常用的缺省值为0.9
推荐使用0.999
Learning rate decay
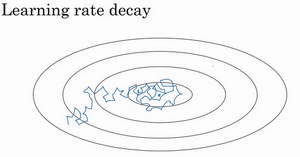 不会精确收敛的原因:用的是固定值,不同的mini-batch中有噪音
衰减:
不会精确收敛的原因:用的是固定值,不同的mini-batch中有噪音
衰减:
local optima
高维容易遇到鞍点
鞍点不是局部最优,问题在于有一段平稳段,上述加速算法能加速这段