1.n
1. j解码器masked:
1. 算一个query不应该看后面的东西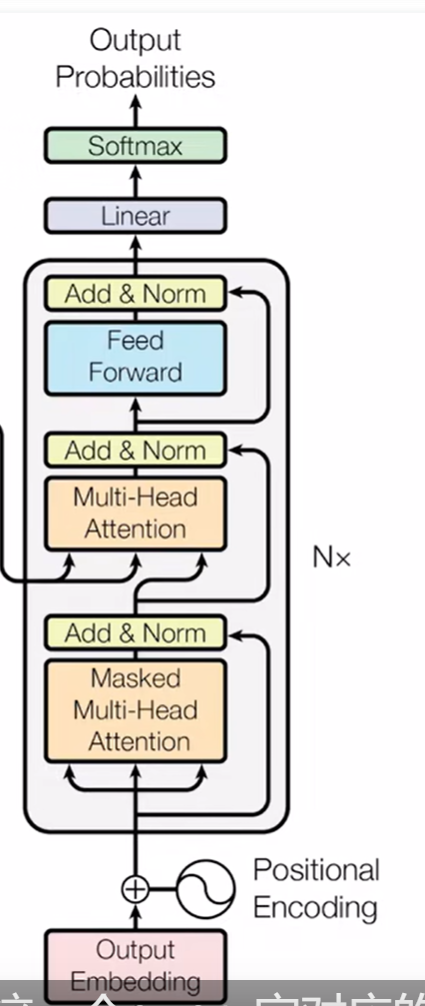
2. encoder的输出作为value,key进来，masked输出作为query
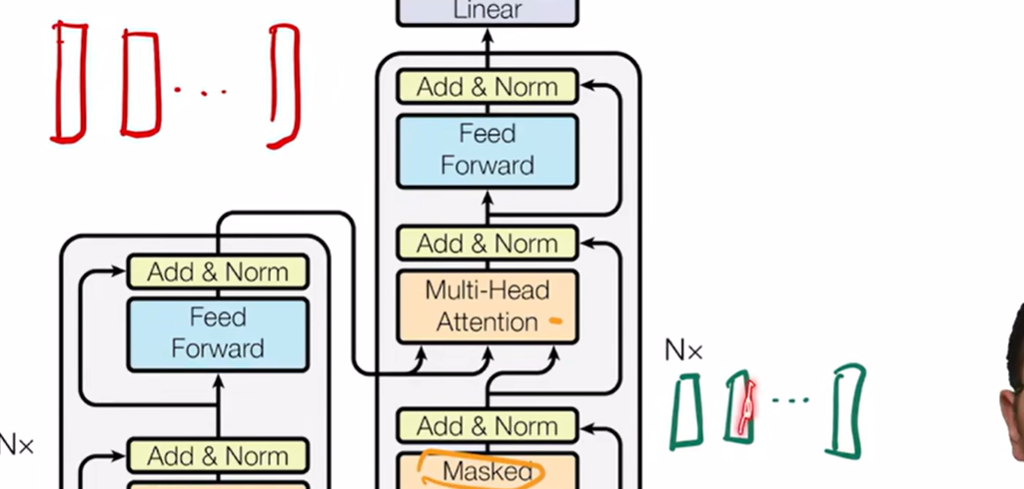对于每个masked输出，算对应的output(来自于value的加权和)
2. feed forwar:
1. MLP 两个线形层
3. RNN 和Transformer一样都是mlp完成语义空间转换，不一样的是如何传递序列，T中是attention获得全局的信息再转换
4. embedding？
5. 在学embedding的时候会把？？？学较小，但position encoding 不会随着长度变长变化 所以×
6.
7. position encoding:在输入的时候加入位置信息
1. 词：用长为512的向量表示
8. multi-head:
1.作用
1. ability to focus on different positions
2. multiple representation subspaces
2. multi attention最后concat
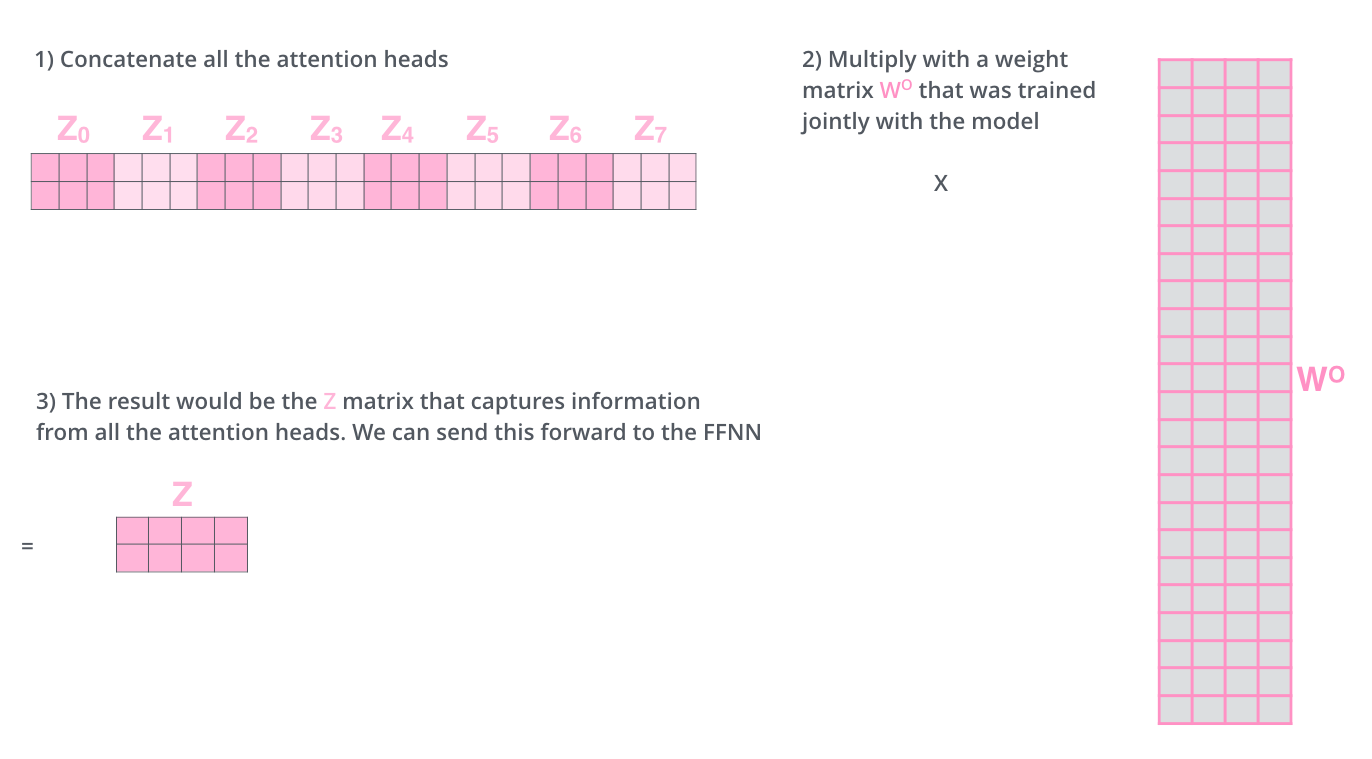
关于维度：
- self-attention Q,K,V维度相同 （n,k)x(k,n) → （n,n)
4. why self-attention
-
矩阵乘法：n*d n*d
第2：顺序计算：下一步计算必须等前面多少步计算完成，越不等并行度越高 （？cnn为什么O(1) 难道sequential意思是一个layer内吗）第3：信息从一个数据点走到另一个数据点需要多久
RNN：计算n次 （d,d)*(d,1)(即MLP) ； 长序列不友好
注：矩阵（A,B)*(B,C)的复杂度是ABC CNN：一个卷积操作 ，并行度很高 path: 如果超过kernel一层层上去是log操作 SA(restricted):query只跟最近的r个邻居做运算，损失path 用的不多
- ？attention对整个模型做了假设更少，导致需要更多数据和更大模型才能训练出来，和RNN和CNN同样效果
Experiment
- regularization
- 大量drop out
- label smoothing (不要到很高的0,1,降调了0.1，虽然不那么确信 但提高accuracy BLEU)
其他
- contiguous
共享内存x = x.permute(0, 2, 1, 3).contiguous()
Q:
- 假设更加一般，所以抓取信息能力变差？→ 需要使用更多数据更大模型才能训练出理想效果
- 为什么
- 如果不除，初始的Attention就会很接近one hot分布，这会造成梯度消失
-
- Softmax函数的特性：Attention权重通常通过softmax函数计算，使得输出总和为1，且各元素非负。当输入向量中某个值远大于其他值时（接近One Hot分布），softmax输出的梯度将极小，几乎为0。
- softmax推导：softmax函数是一个广泛使用的激活函数，尤其在处理多类分类问题时，它可以将任意实数向量转换为一个概率分布。softmax函数定义如下：
-
- 如果不除，初始的Attention就会很接近one hot分布，这会造成梯度消失
如果有一个向量 ( z )，则对于向量中的每个元素 ( z_i )，softmax函数 ( \sigma(z)_i ) 的定义为： [ \sigma(z)i = \frac{e^{z_i}}{\sum{j} e^{z_j}} ]
现在我们来推导softmax函数关于输入 ( z ) 的梯度。首先，定义 ( z ) 的softmax输出为 ( y )，其中 ( y_i = \sigma(z)_i )。
我们需要计算 ( \frac{\partial y_i}{\partial z_k} )，即 ( y_i ) 关于每个输入 ( z_k ) 的偏导数。根据softmax的定义，我们可以有以下推导：
-
当 ( i = k ) 时，即计算 ( \frac{\partial y_i}{\partial z_i} ): 使用链式法则，我们得到： [ \frac{\partial y_i}{\partial z_i} = \frac{e^{z_i} \sum_{j} e^{z_j} - e^{z_i} e^{z_i}}{(\sum_{j} e^{z_j})^2} = \frac{e^{z_i}}{\sum_{j} e^{z_j}} \left(1 - \frac{e^{z_i}}{\sum_{j} e^{z_j}}\right) = y_i (1 - y_i) ]
-
当 ( i \neq k ) 时，即计算 ( \frac{\partial y_i}{\partial z_k} )： [ \frac{\partial y_i}{\partial z_k} = \frac{\partial}{\partial z_k}\left(\frac{e^{z_i}}{\sum_{j} e^{z_j}}\right) ] 因为 ( z_i ) 与 ( z_k ) 是不同的输入，所以 ( e^{z_i} ) 对 ( z_k ) 的偏导数为0： [ \frac{\partial y_i}{\partial z_k} = \frac{0 - e^{z_i} e^{z_k}}{(\sum_{j} e^{z_j})^2} = -\frac{e^{z_i}}{\sum_{j} e^{z_j}} \frac{e^{z_k}}{\sum_{j} e^{z_j}} = -y_i y_k ]
因此，softmax函数 ( y_i ) 关于 ( z_k ) 的偏导数可以总结为： [ \frac{\partial y_i}{\partial z_k} = y_i (\delta_{ik} - y_k) ] 其中，( \delta_{ik} ) 是克罗内克函数，当 ( i = k ) 时值为1，否则为0。
这个导数形式对于实现softmax的反向传播非常重要，它描述了输出 ( y_i ) 对输入 ( z ) 的每个成分 ( z_k ) 的依赖关系和调整方式。