Train/dev/test
总体数据更大,需要更少的dev/test
dev/test come from same distribution test: 目的是对模型做出无偏估计,如果不需要无偏估计,则不需要test,在dev上测试迭代。为什么dev不能无偏估计:因为在模型选择和调参过程中,验证集被重复使用,每次根据验证集调整参数会使模型简介学习这部分数据→对验证集产生过拟合
Bias/Variance
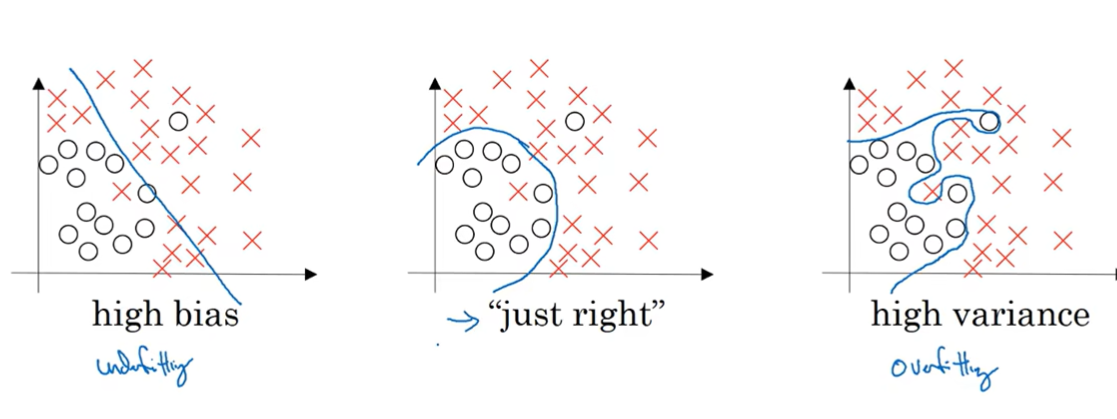

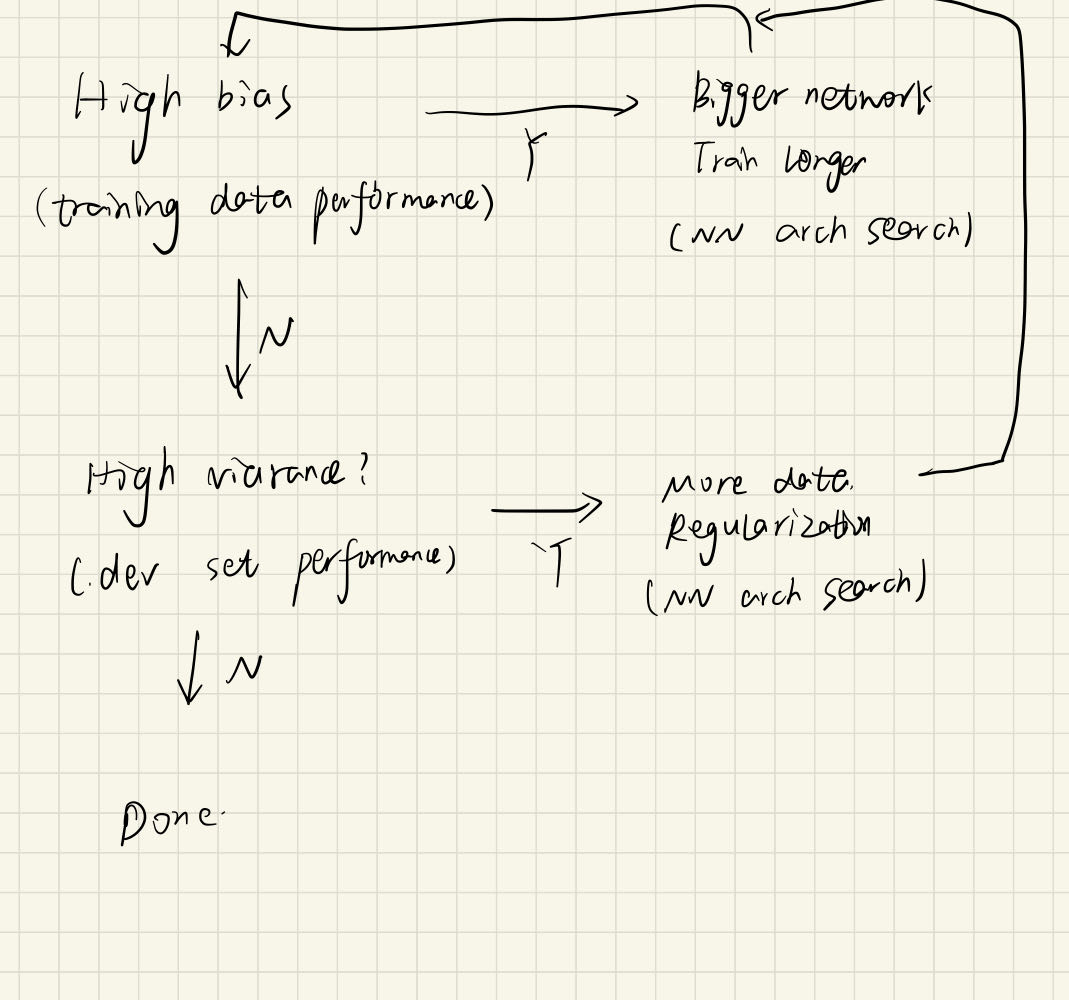
Bias Variance tradeoff:在早期很难同时降低,现在可以(所以对supervised learning 大有裨益, 如果是regularized,那么训练一个更大的网络没有坏处
Regularization
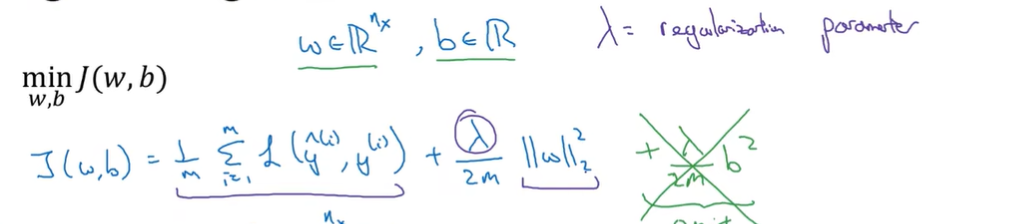
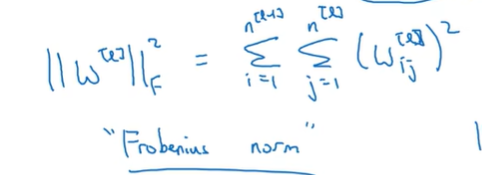 这里矩阵范数称为Frobenius norm 而不是二范数
这里矩阵范数称为Frobenius norm 而不是二范数
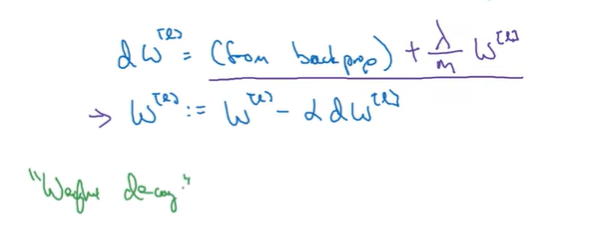
 因此L2-regularization被称为weight decay,相当于w乘了减小的系数
因此L2-regularization被称为weight decay,相当于w乘了减小的系数
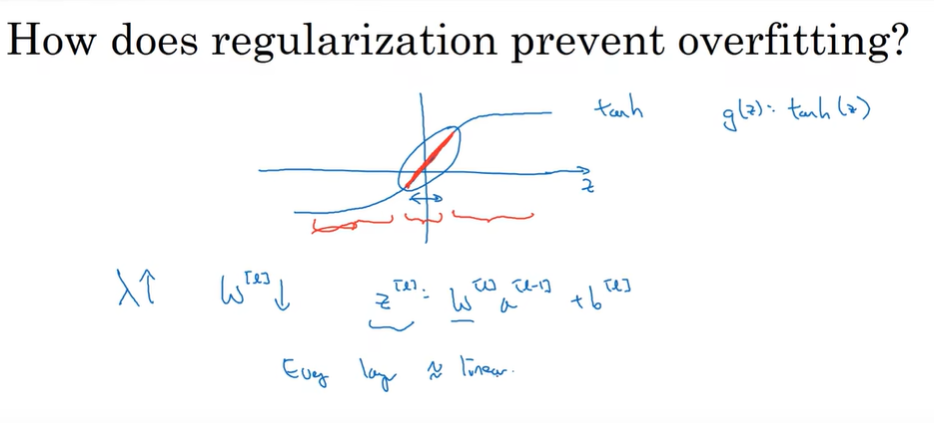
变大,cost func 里面w需要变小,z变小,就会集中在中间小区域,呈相对线性,不容易过拟合
Dropout regularization
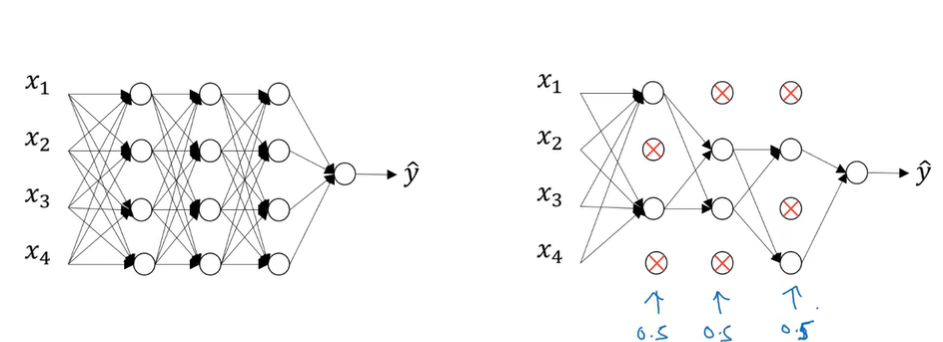 随机dropout
最常见:inverted dropout
随机dropout
最常见:inverted dropout

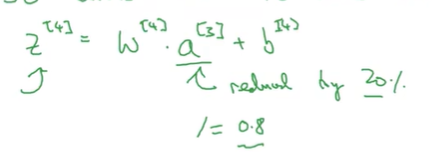 Q:为什么最后除0.8: 因为减少20%后,我们希望z的期望不变。
证明在test data运用inverted dropout,使数据扩展问题变少
test time没有drop-out,因为用dropout会受到干扰
Q: 为什么dropout work: 每次随机清除一些节点,不会依赖于任何一个feature,需要spread out weights, 使有一个shrink weights 的效果,类似于L2正则化。通常对input layer 不进行dropout.在cv用的很多因为像素作为特征很多。如果假如dropout, cost func J 没明确定义很难计算,所以画损失函数图没法画损失了debug工具。调试时设置keep-prob为1,保留所有参数,确保J单调递减
Q:为什么最后除0.8: 因为减少20%后,我们希望z的期望不变。
证明在test data运用inverted dropout,使数据扩展问题变少
test time没有drop-out,因为用dropout会受到干扰
Q: 为什么dropout work: 每次随机清除一些节点,不会依赖于任何一个feature,需要spread out weights, 使有一个shrink weights 的效果,类似于L2正则化。通常对input layer 不进行dropout.在cv用的很多因为像素作为特征很多。如果假如dropout, cost func J 没明确定义很难计算,所以画损失函数图没法画损失了debug工具。调试时设置keep-prob为1,保留所有参数,确保J单调递减
其他防过拟合
- data augmentation
- early stopping
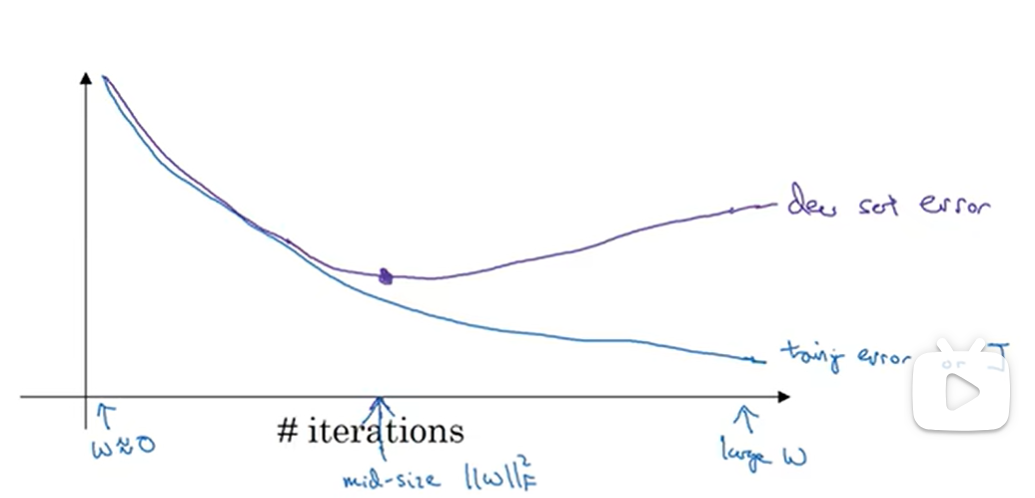
- 最初w 很小,到最后w参数变得很大,在中间停止迭代会得到一个mid-size ,类似于L2正则化
- 缺点:不能独立处理这两个问题,提早停止使得J不够小
- 如果用l2正则化,需要训练的时间很长(makes the search space of hyper parameters easier to decompose,easier to search over??),但是需要探索很多,计算代价太高,用early stop只用一次梯度下降
归一化输入
用mean variance 归一化:
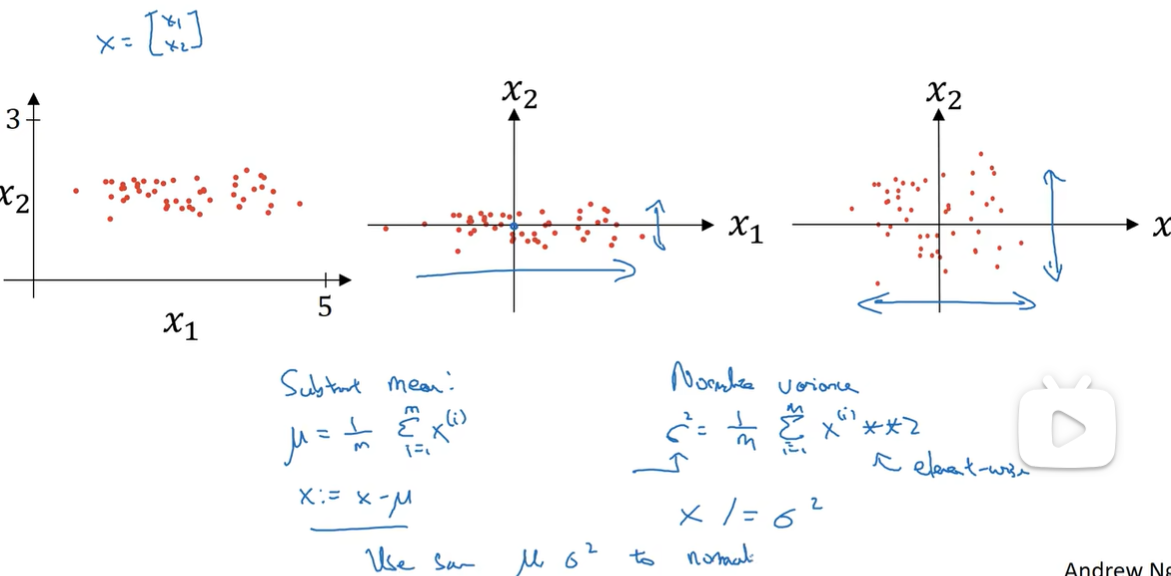 注意:如果用mean var归一化训练集,也需要用同样mean var归一化测试集,因为希望用相同的数据转换
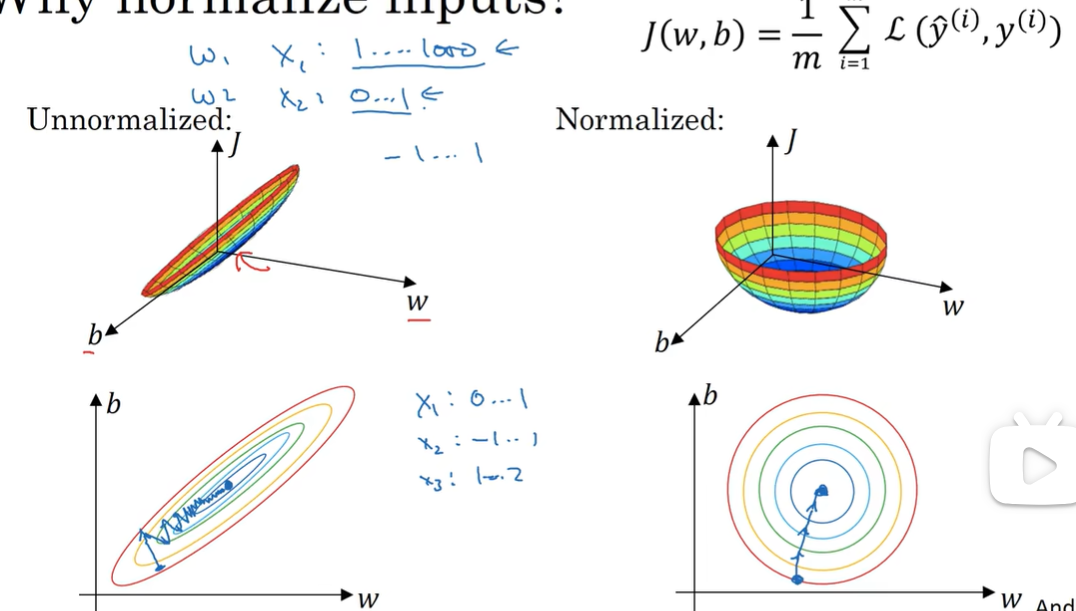
Q:为什么?:如果 范围相差很大,那么也相差很大,如左图很狭长需要多次迭代过程;所以归一化更容易去优化
注意:如果用mean var归一化训练集,也需要用同样mean var归一化测试集,因为希望用相同的数据转换
Q:为什么?:如果 范围相差很大,那么也相差很大,如左图很狭长需要多次迭代过程;所以归一化更容易去优化
梯度消失梯度爆炸
解决:
- 权重初始化
 relu设置左下,tanh 设置右边
relu设置左下,tanh 设置右边
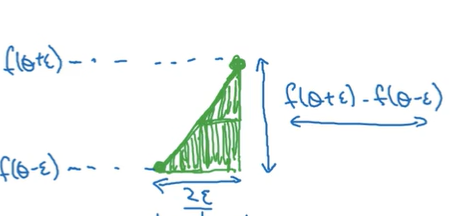
逼近导数:
- 双边误差
- 误差 → 更准确
- 误差 →不够准确
- 误差 → 更准确
梯度检验
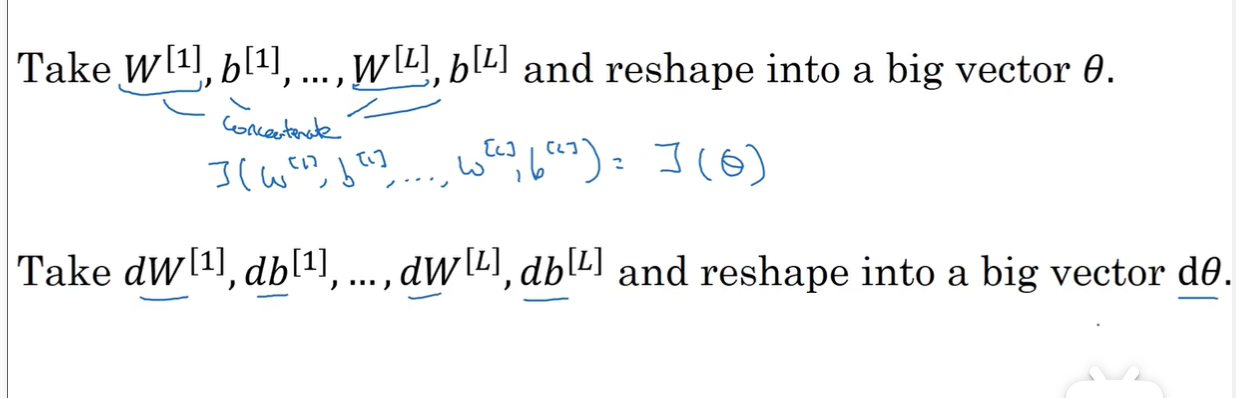
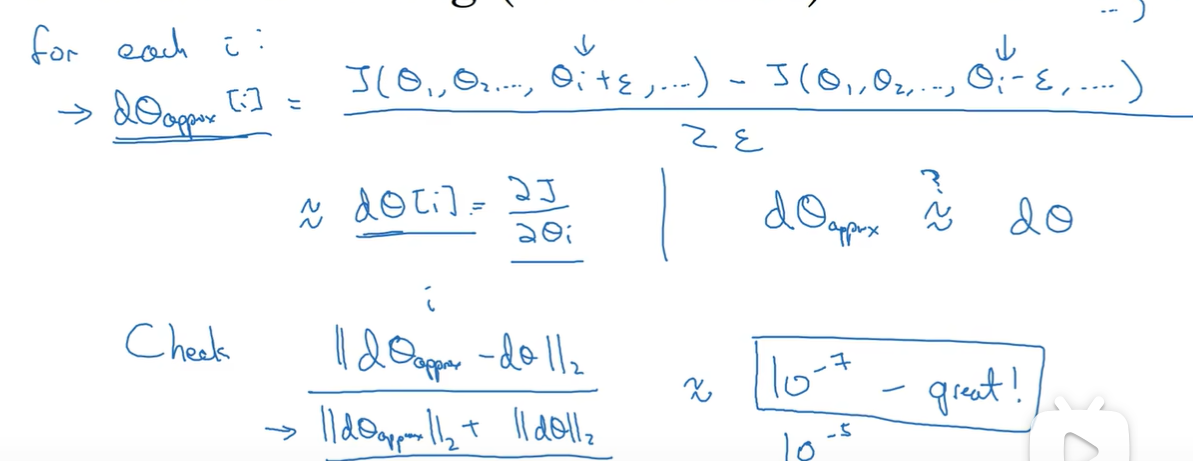
分母是类似归一化,检查最后的误差
梯度检验实现
- 不要在训练中使用梯度检验,只用于debug
- 找到哪项参数导数计算有问题
- 需要regularization
- 不能用dropout
 意思是会有偶然性在某个区间有问题,需要随机初始化或者训练一段时间后再检验减少这种偶然
意思是会有偶然性在某个区间有问题,需要随机初始化或者训练一段时间后再检验减少这种偶然