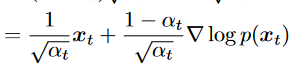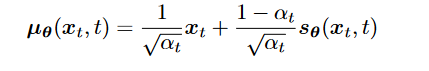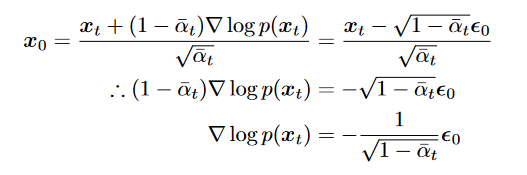Links:
unified version
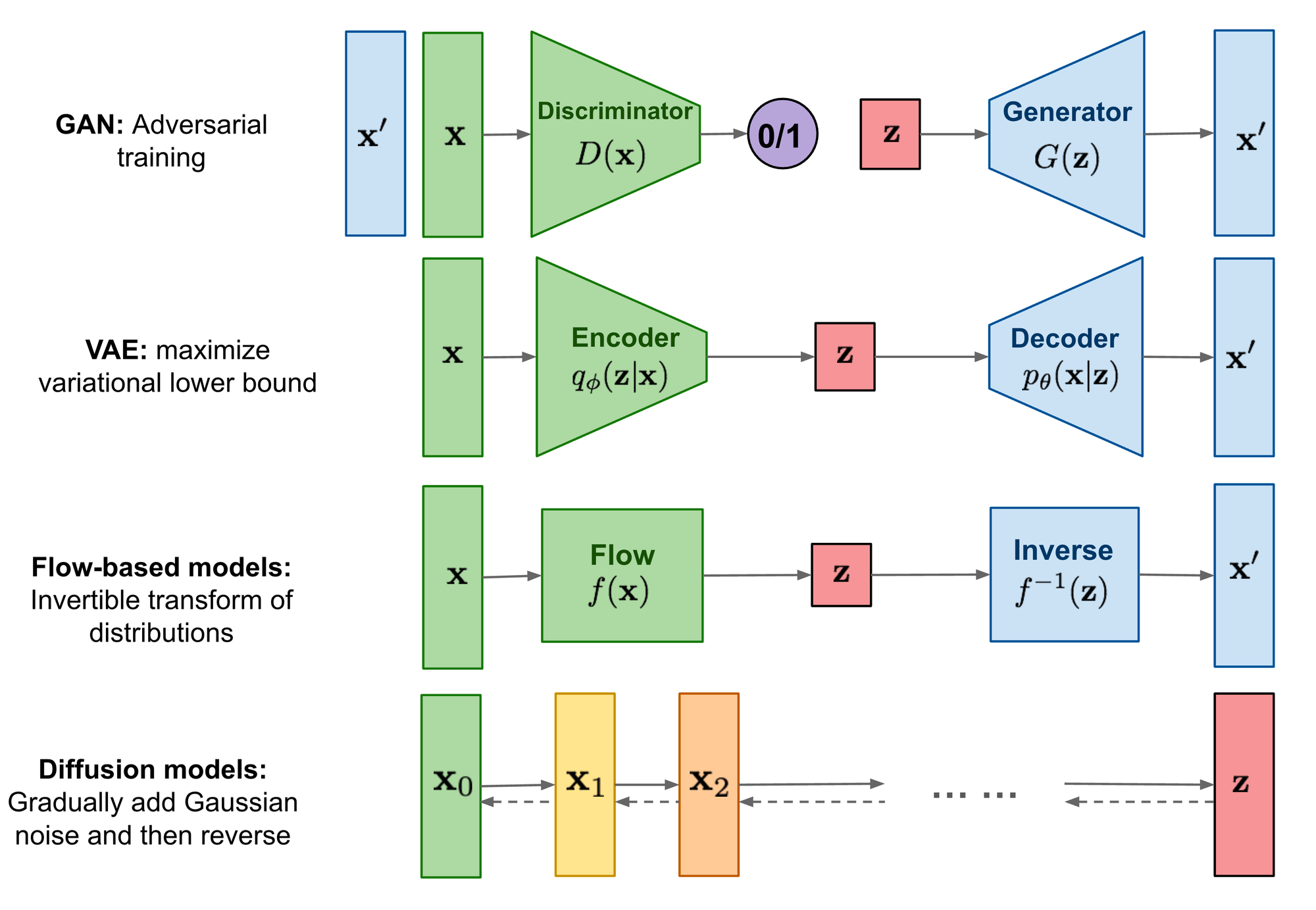
Intro
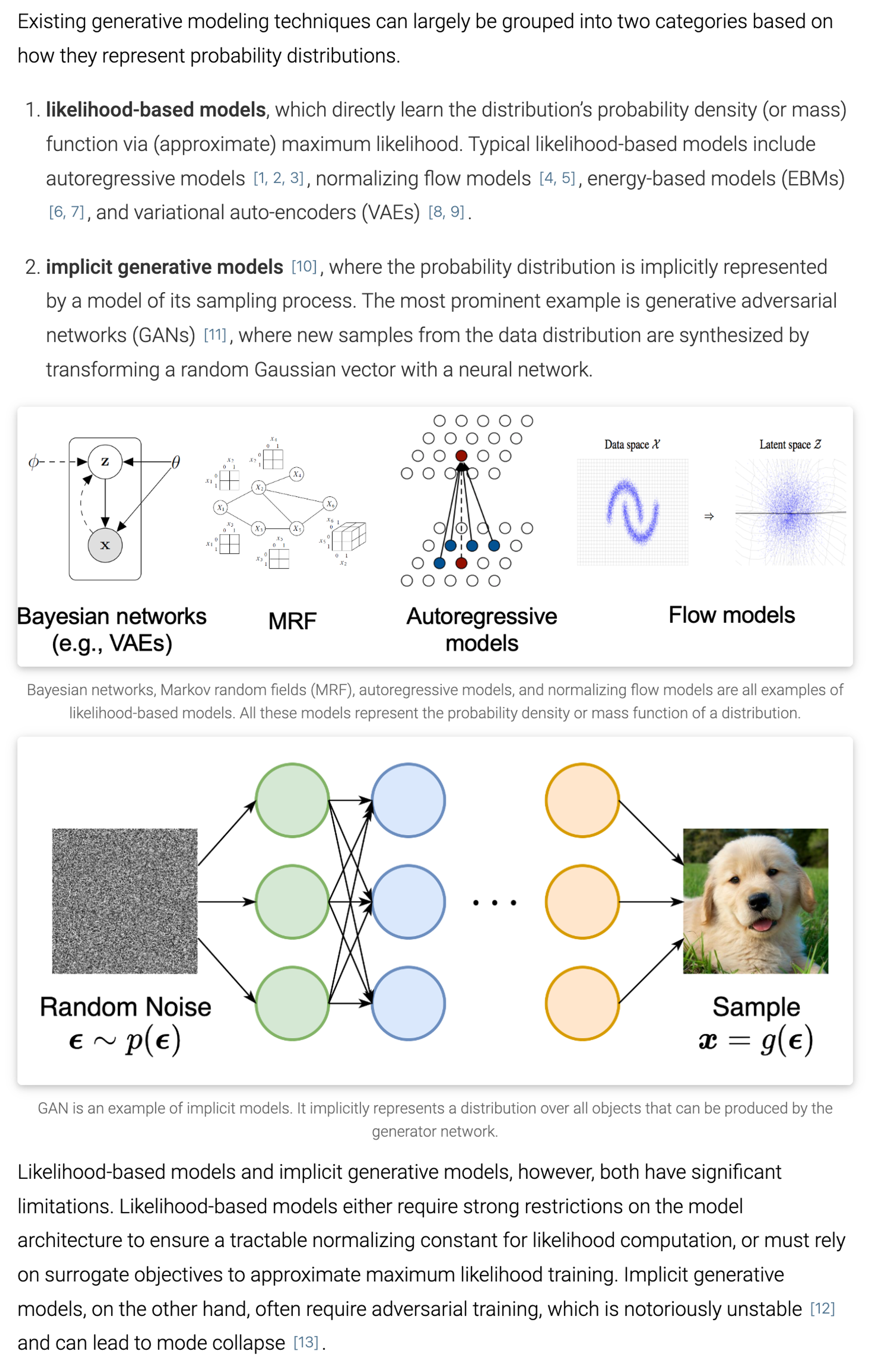
- generative model:
- given samples x → learn true data distribution p(x)
- 哪些
- gan
- likelihood-based :assigns a high likelihood to the observed data samples.
- vae
- energy-based : a distribution is learned as an arbitrarily flexible energy function that is then normalized.
- score-based: instead of learning to model the energy function itself, they learn the score of the energy-based model as a neural network.
quote from Yang Song
BG
- generated by latent variable
- generally learn low-dim latent representations
ELBO
-
: model the latent variable and the data, likelihood-based: maximize the likelihood .
-

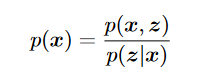
-
推导evidence lower bound:(VLB ELB)
 KL大于0, : the approximate posterior.p(x):likelihood of observed or generated data
KL大于0, : the approximate posterior.p(x):likelihood of observed or generated data- 当KL趋近于0意味着logp(x)接近于ELBO式。如果减小KL距离,则q接近真实后验分布。但因为我们不知道真实后验,所以KL很难计算。而左侧p(x)与参数无关,所以optimize ELBO就等于使得估计的后验 接近真实的后验。并且因为KL趋近于0,可以用ELBO估计p(x)
VAE

- maximize ELBO

- encoder learn , decoder learn
- 式子
- reconstruction likelihood of decoder:确保decoder对latent有效建模
- 学习到的 z 分布(variational distribution) (q(z|x))和先验相似程度。确保encoder有效建模而不是一个Dirac函数
- encoder: 学习一个multi gaussion, 假设prior是standard gaussion:
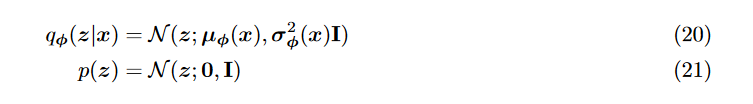
- reconstruction term 可以用monte varlo估计,latents are sampled from .单纯sample是不可导的→ reparamterization trick
- reparamterization trick: 将r.v.重写做noise variable函数,从而化为从一个standard gaussioan 中sample,能够对参数做gradient descent.(注意 element-wise product)
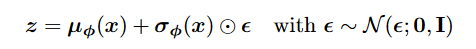
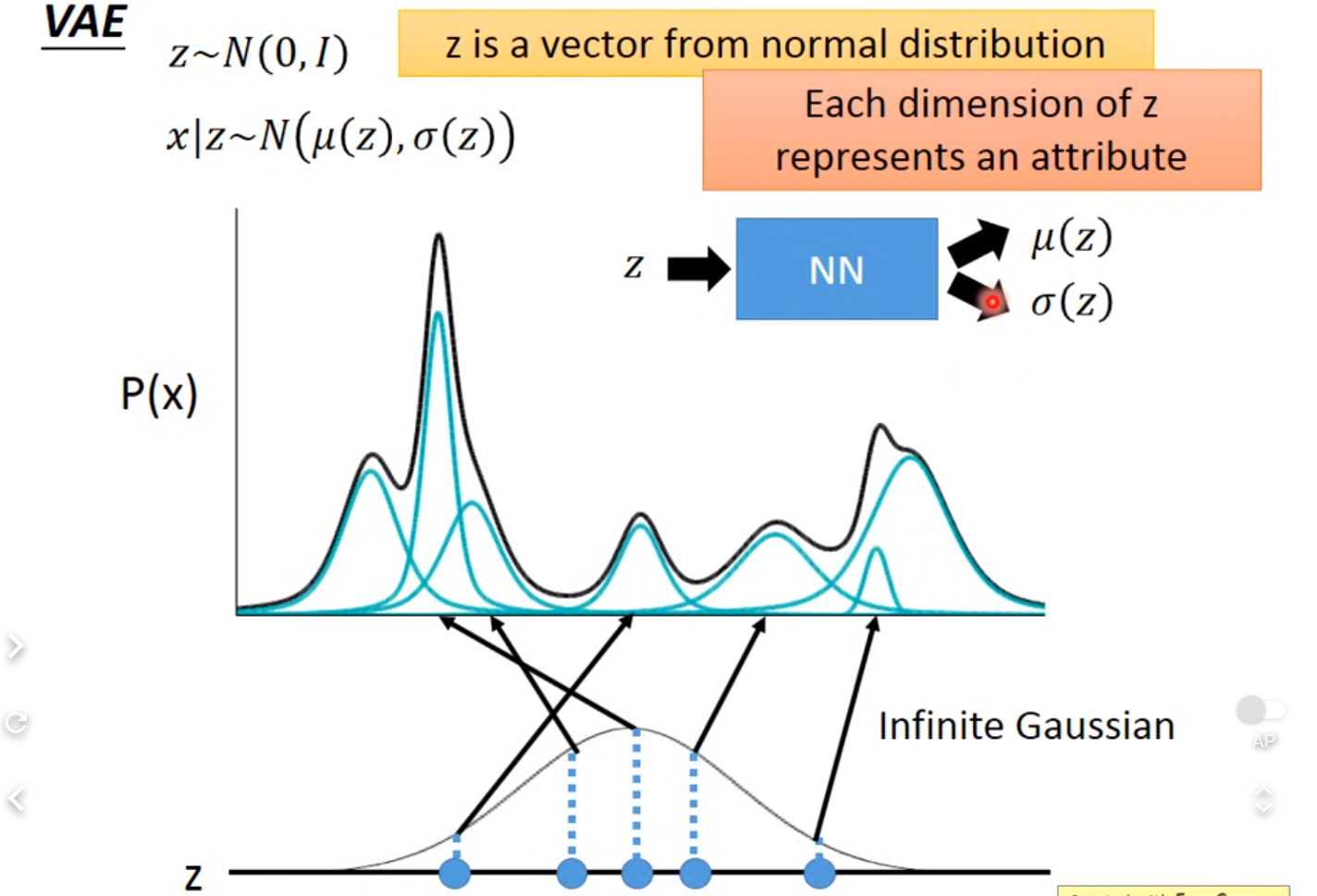
- VAE中 z dim 小于x→学到compact latent vector, 可修改latent vector控制生成
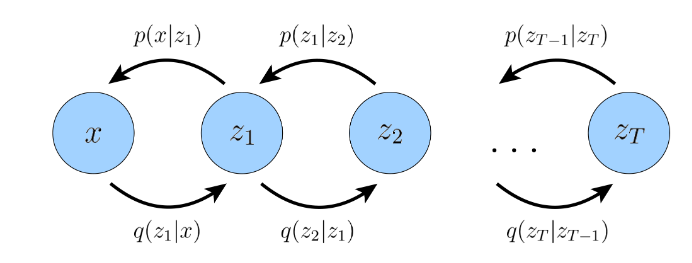
HVAE
将前向反向都看作为马尔科夫链: decoding each latent only conditions on previous latent , 低级依赖高级
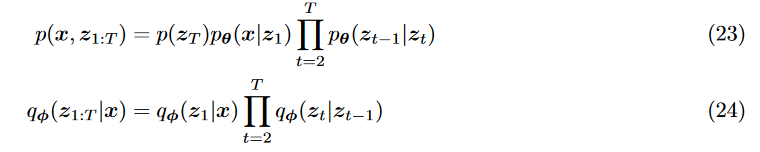 Lower-bound:
Lower-bound:
Variational Diffusion Models
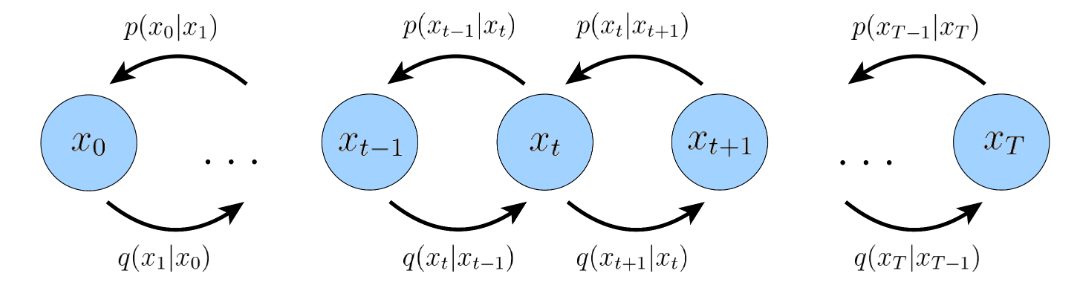
- 与HVAE不同
- latent dim = data dim (所以latent 和data 都写作 )
- at t, the latent encoder is defined as a linear Gaussian model
- The Gaussian parameter of latent encoder vary → at final T, standard Gaussian
- the distribution of each latent variable in the encoder is a Gaussian centered around its previous hierarchical latent.
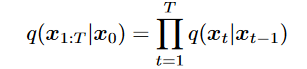
- linear Gaussian parameters: hyperparameters or learned
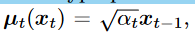
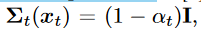
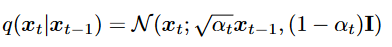
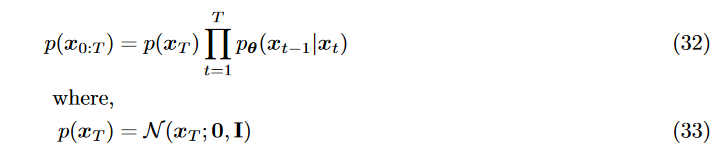
- 不同于HVAE, encoder过程没有参数 ,每一步为Gaussian. 我们关心 以生成新的.
- ELBO式子

- reconstruction:
- prior matching : 不用优化,没有learnable parameters, 足够大T可以使最后为gaussian, 这一项变为0
- consistency term: 因此主要优化第三个式子, 然而使用Monte Carlo涉及两个r.v. , 会变得不稳定(这两个随机变量噪声叠加,最终估计的是加上所有采样,所以variance 会高)
- 由于无法求(注:推导 :是 given ,如果将看作 那么后面就是边缘概率的积分) 利用markov化为另一种形式
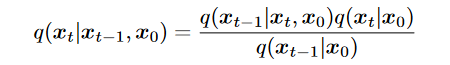
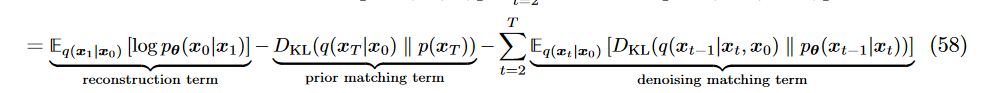 1. 最后一项:denosing matching. 希望denosing transition step 和 ground-truth denosing transition step 越接近越好。其中在HVAE由于本身encoder learning复杂因此不好计算,而在VDM中可以利用gaussian性质简化:
1.
1. 最后一项:denosing matching. 希望denosing transition step 和 ground-truth denosing transition step 越接近越好。其中在HVAE由于本身encoder learning复杂因此不好计算,而在VDM中可以利用gaussian性质简化:
1. 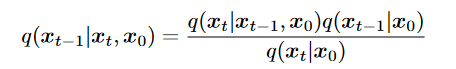 这样可以用markov, 只需要找到就可以。
这样可以用markov, 只需要找到就可以。
2.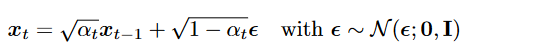
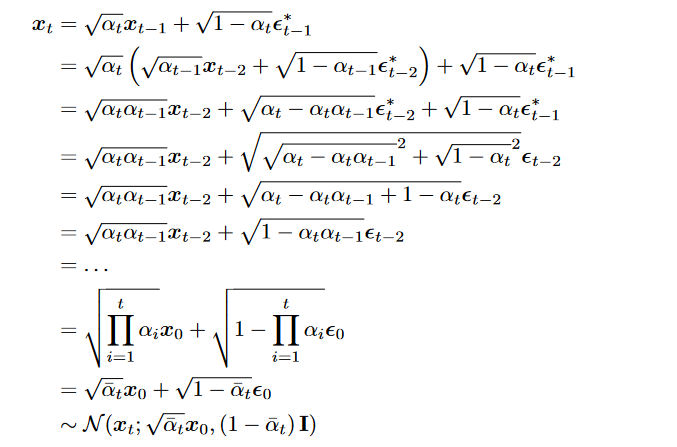 3. 最终化为
3. 最终化为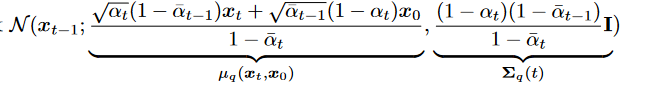 2. 由于 希望denosing transition step 和 ground-truth denosing transition step 越接近越好,可以把 建模为Gaussian :
2. 由于 希望denosing transition step 和 ground-truth denosing transition step 越接近越好,可以把 建模为Gaussian :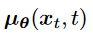 , mean确定后参数确定,从而variance确定
1.
, mean确定后参数确定,从而variance确定
1. 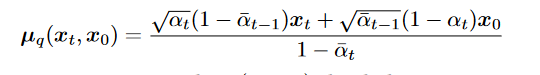
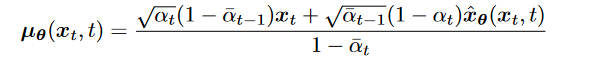 由 neural network给出
2.
由 neural network给出
2. 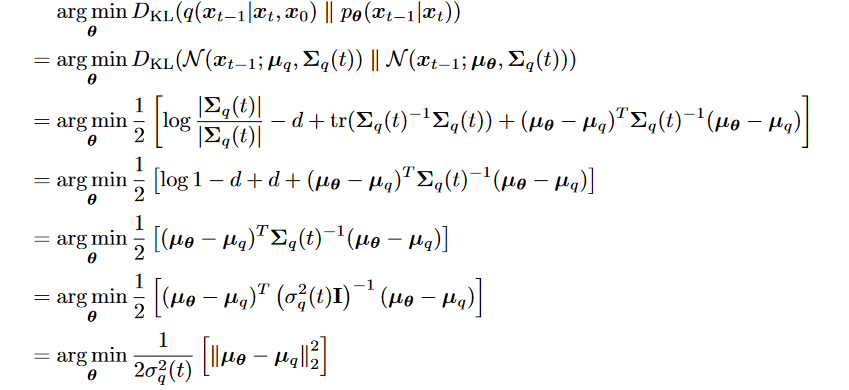 3.
3. 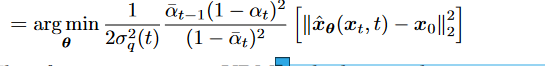 4. 最后是minimize expectations over all timesteps
4. 最后是minimize expectations over all timesteps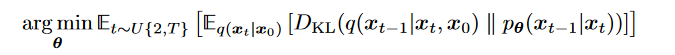
- Learning noise parameters
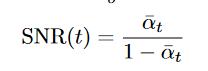 由前面推导得SNR,SNR越小Noise越大,希望t增加snr单调减少。
由前面推导得SNR,SNR越小Noise越大,希望t增加snr单调减少。- 最终可化简为
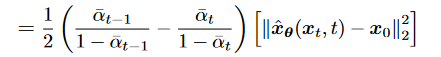
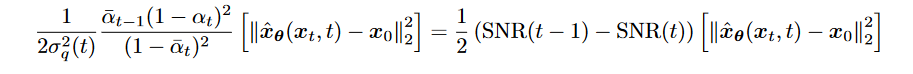
- 希望构建nn去model snr, 表达为
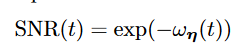
- noise形式
- 带入
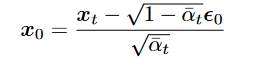 到 , 得
到 , 得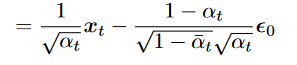
- 带入KL式
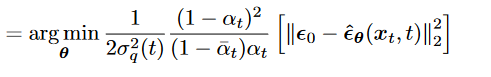
- 表示predict x0相当于predict noise.(一些表明predict noise performance更好)
- 带入
- 形式
- Tweedie’s Formula : “states that the true mean of an exponential family distribution, given samples drawn from it, can be estimated by the maximum likelihood estimate of the samples (aka empirical mean) plus some correction term involving the score of the estimate.” 矫正项考虑到sample分布情况
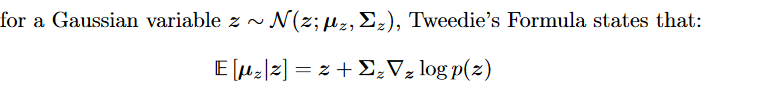
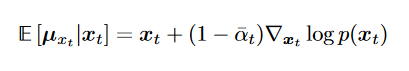
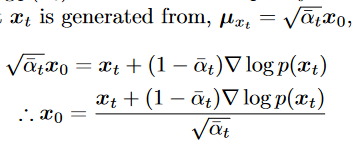
- 带入 推出:
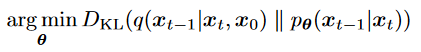
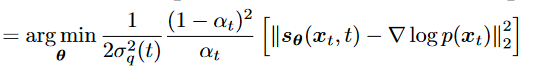 is a nn learns to predict the score function
is a nn learns to predict the score function - 和原来 关系?:可见多一个scale项,score function 指导我们如何在数据空间中移动以优化(最大化)目标函数(这里是log p)的作用,intuitively,是添加source noise 的反方向
- Tweedie’s Formula : “states that the true mean of an exponential family distribution, given samples drawn from it, can be estimated by the maximum likelihood estimate of the samples (aka empirical mean) plus some correction term involving the score of the estimate.” 矫正项考虑到sample分布情况
总结
扩散
反向
 注:
注:
score-based generative models
- energy-based model:
- 任意 distribution表示:
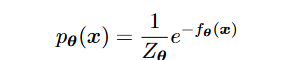 其中是energy function, model by nn
其中是energy function, model by nn - 是normalization 项 ,很难计算,用log p计算梯度去除了normalization项(一个常数项)
- sample过程:
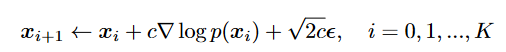 score function指示我们如何走直到一个mode.添加噪声 加入随机化,避免生成时总到一个mode
score function指示我们如何走直到一个mode.添加噪声 加入随机化,避免生成时总到一个mode
- 任意 distribution表示:
- 挑战
- the score function is ill-defined when x lies on a low-dimensional manifold in a high-dimensional space. 自然图像从像素上来说是高维的,但处于低维流形中(往往符合内在一些规律,可以用低维表示核心信息。而不在低维流形的点是零概率,因此log不定义。
- 在low density regions 期望不准确。(即对于rarely seen 或unseen )
- Langevin dynamics 不能算混合的概率,log后丢失系数
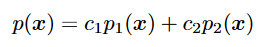
- 混合高斯,尽管右下到达概率大,丢失系数后还是以同等概率到达
- 方法:
- adding multiple levels of Gaussian noise to the data.
- 避免处于低维流形
- 对每个mode 增加了覆盖的地方,
- ??” Lastly, adding multiple levels of Gaussian noise with increasing variance will result in intermediate distributions that respect the ground truth mixing coefficients.
- adding multiple levels of Gaussian noise to the data.
Guidence( Conditional )
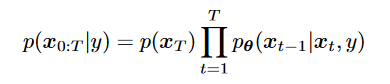 y: a text encoding in image-text generation, or a low-resolution image
learn:
y: a text encoding in image-text generation, or a low-resolution image
learn: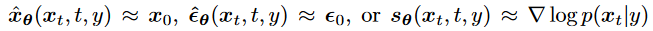 guidence: 普通方法训练conditional diffusion时会忽视给定条件信息,guidence提供更加准确的指导但以牺牲diversity为代价
guidence: 普通方法训练conditional diffusion时会忽视给定条件信息,guidence提供更加准确的指导但以牺牲diversity为代价
classifier guidance

- unconditional score: 像之前一样learn
- adv gradient : 训练一个classifier, 输入,输出
- sample时 :计算两者和
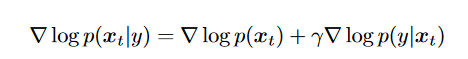
- 系数控制conditional的情况
- 缺点:依赖于classifier, (因为需要处理任意的noisy inputs, pretrained model不能用,需要临时训练)
classifier-free guidance
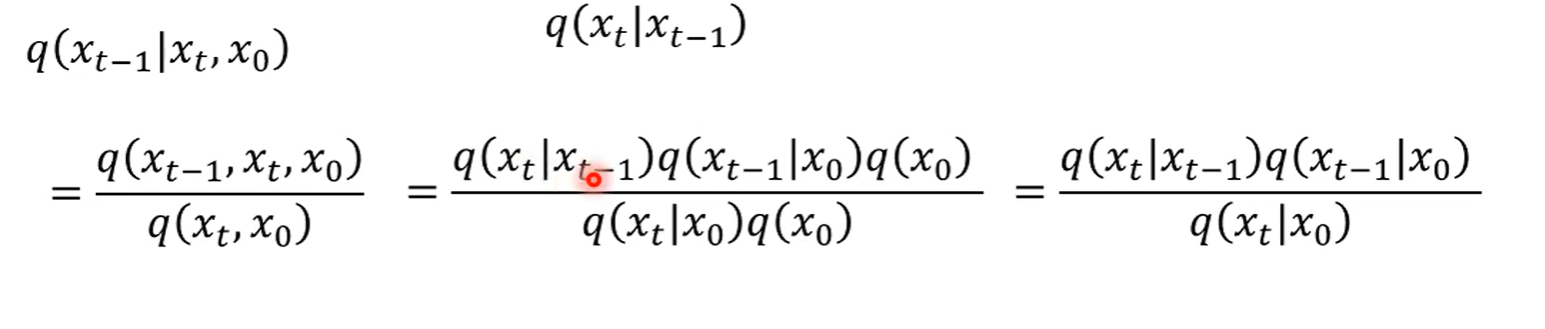
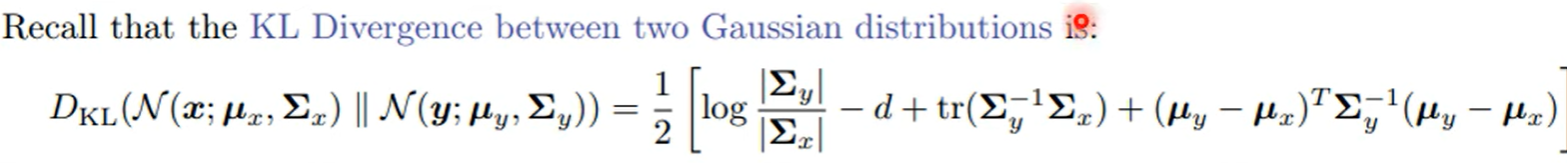
VAE
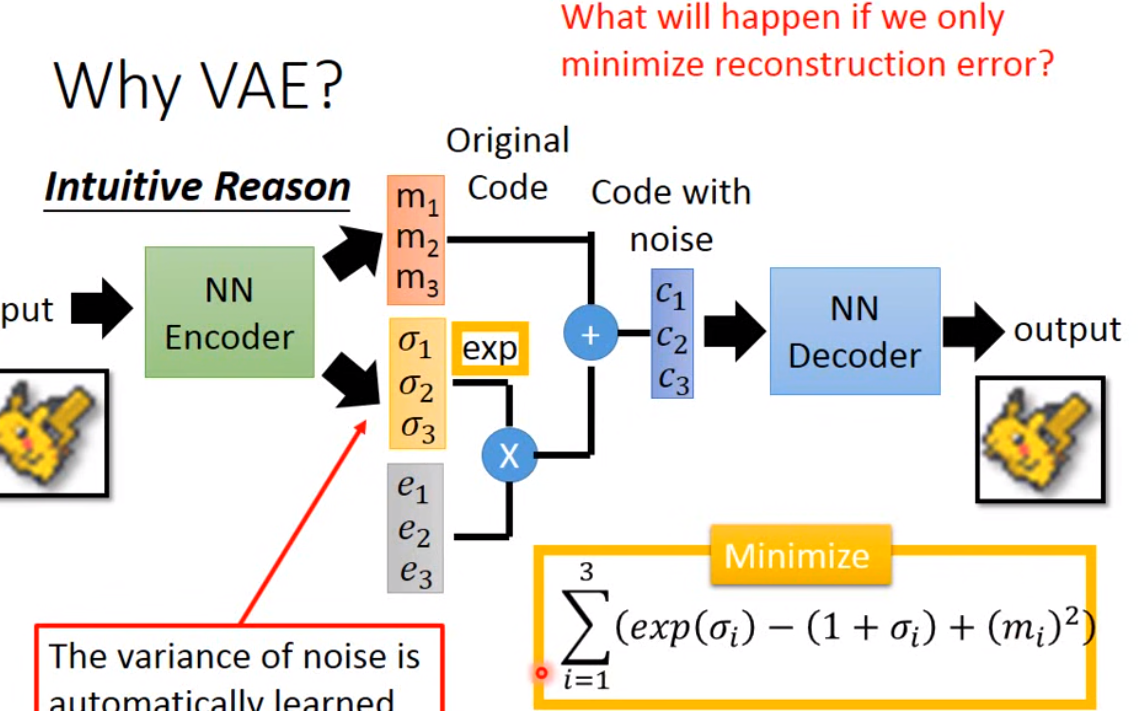 Intuitive:
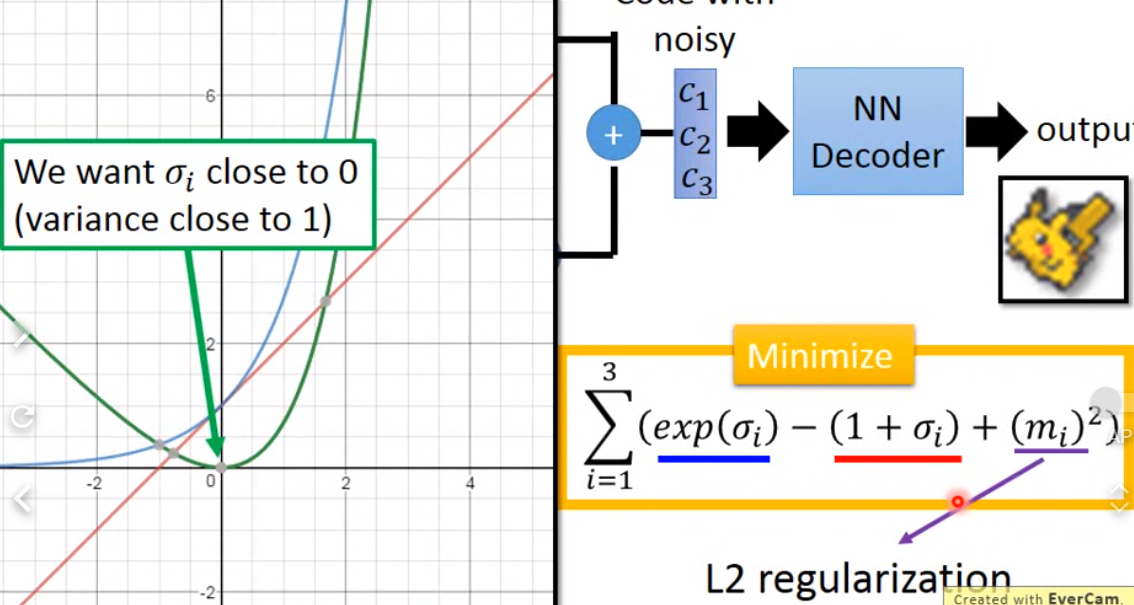
sigma 表示vatiance(exp()表示限制为正数,即可以表示为variance), e是从nomral distribution中sample,相乘加到原来的m上就是noise. 但是你单单训练reconstruction error是不行的,他会自动觉得variance越小越好(不会有不同code信息,reconstruction error最小),需要限制variance不可以太小
Intuitive:
sigma 表示vatiance(exp()表示限制为正数,即可以表示为variance), e是从nomral distribution中sample,相乘加到原来的m上就是noise. 但是你单单训练reconstruction error是不行的,他会自动觉得variance越小越好(不会有不同code信息,reconstruction error最小),需要限制variance不可以太小
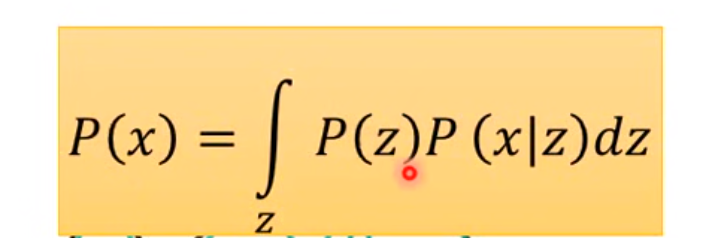
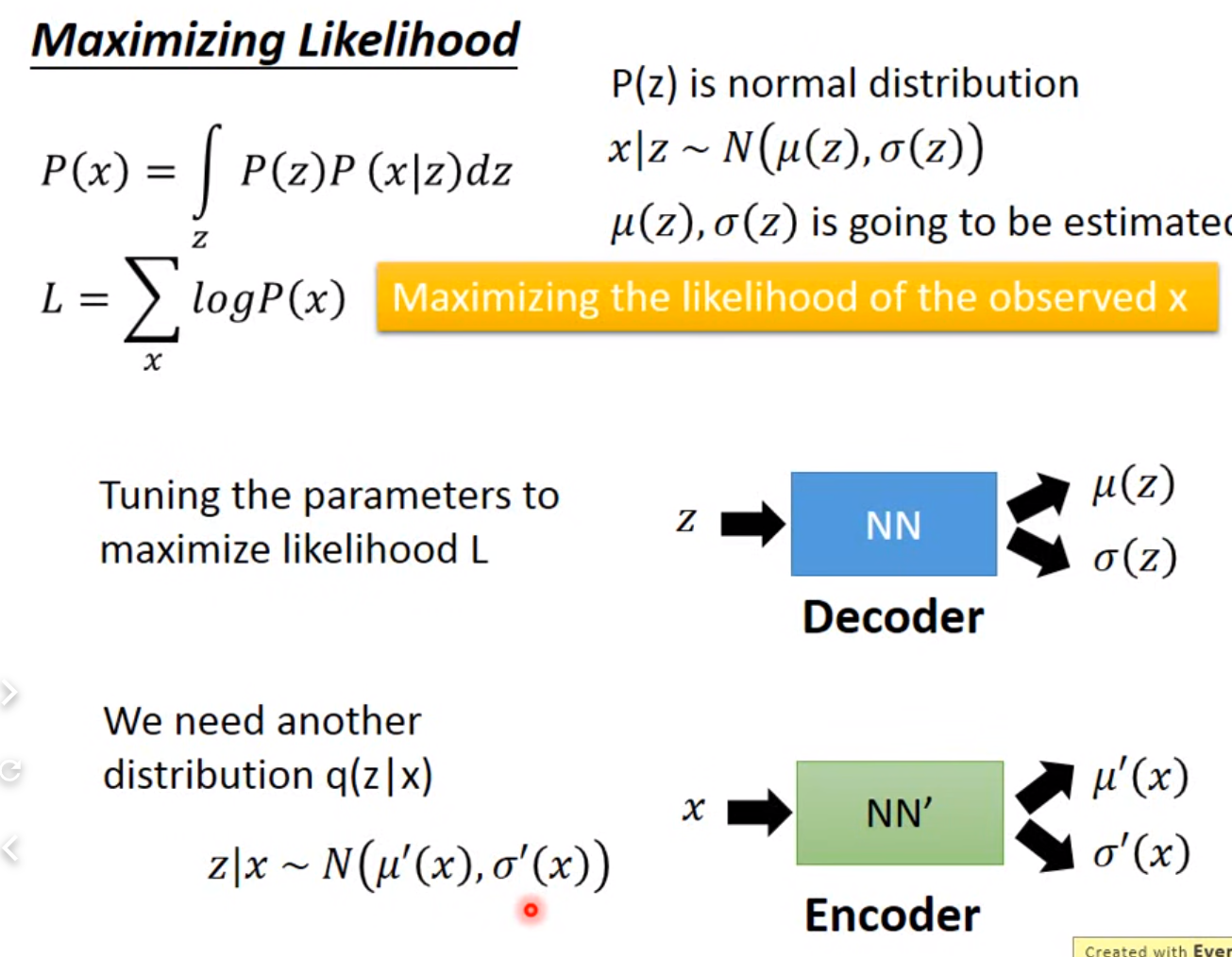

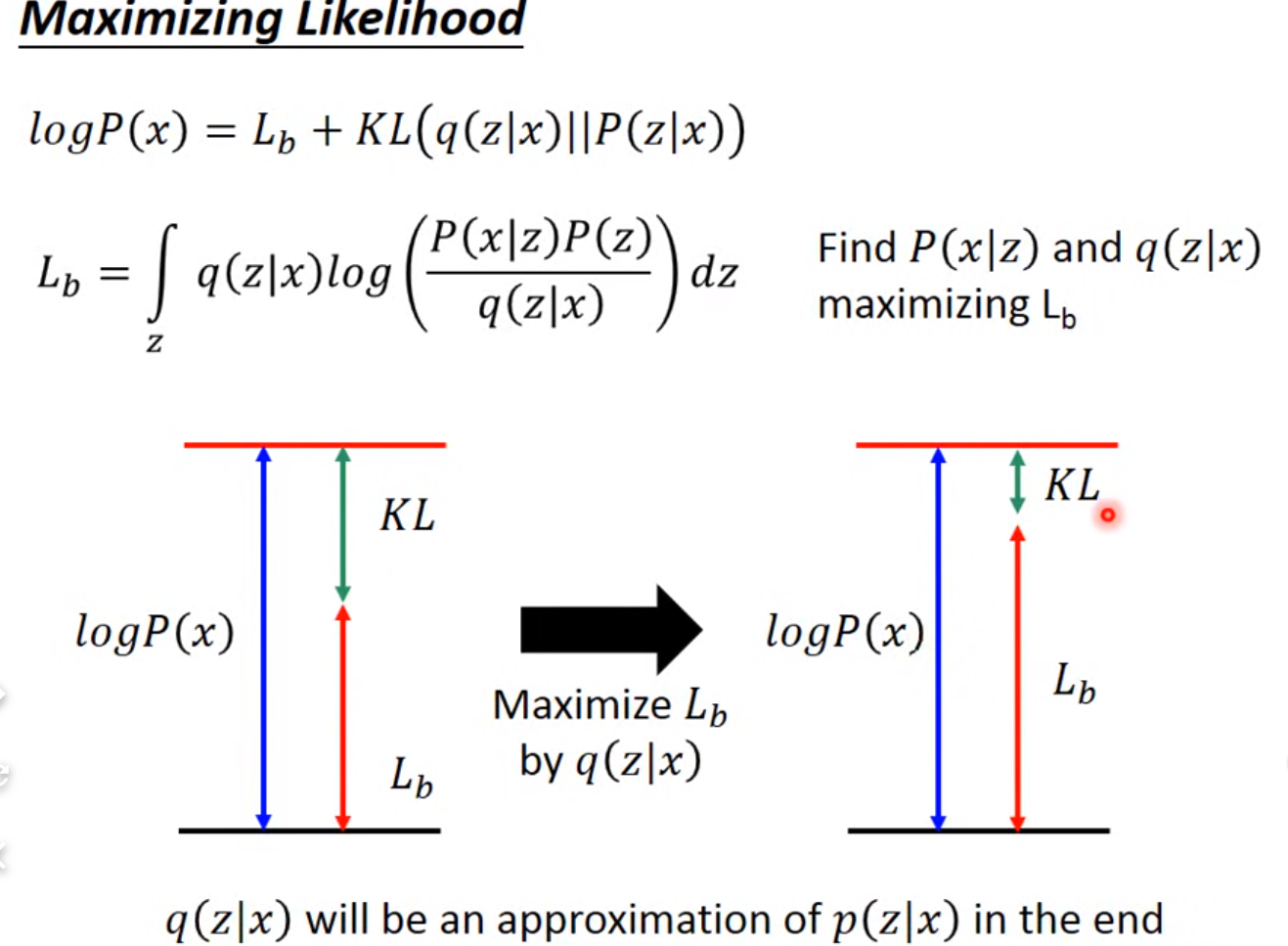
maximize likelihood 就是 最大Lb
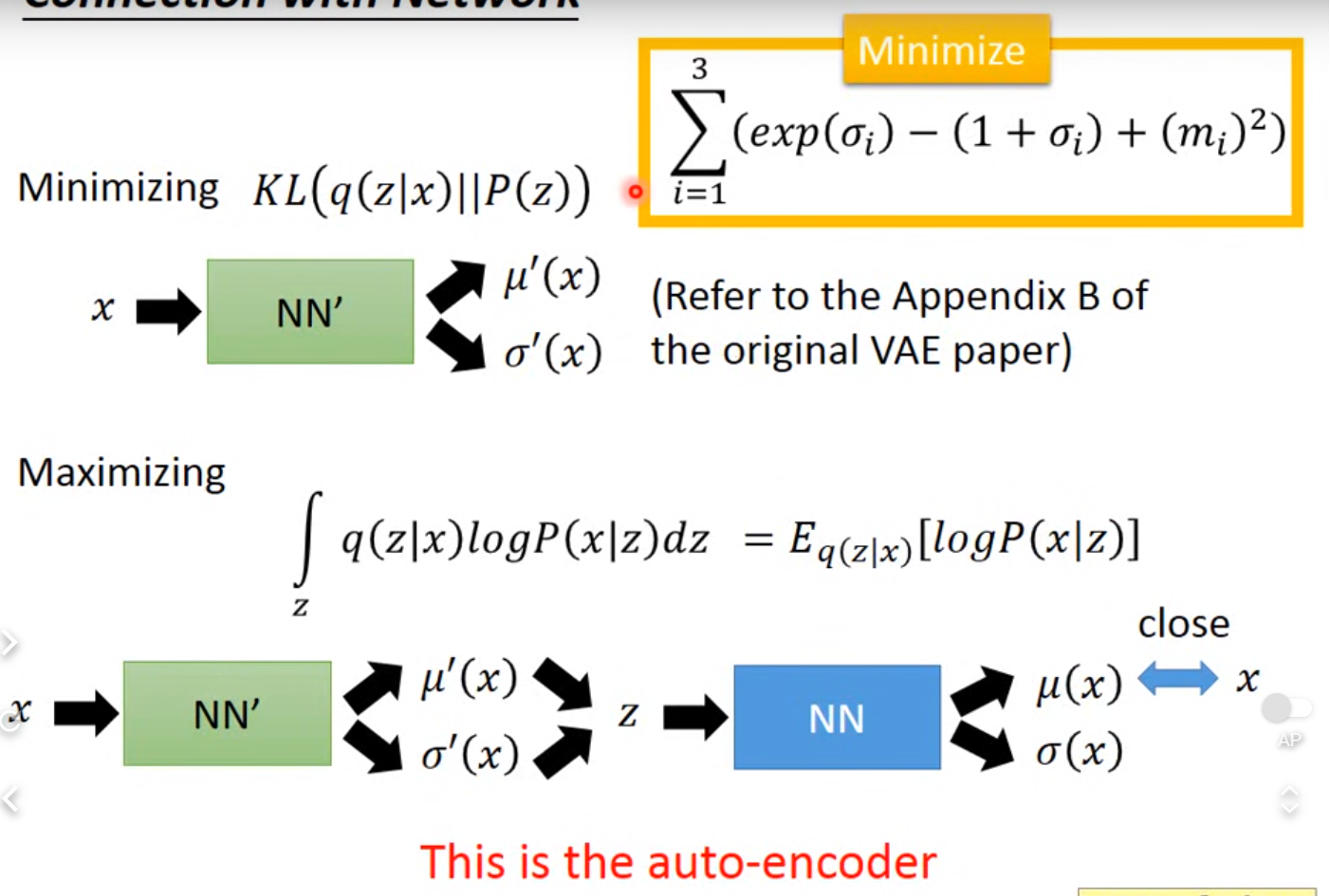
VAE问题:
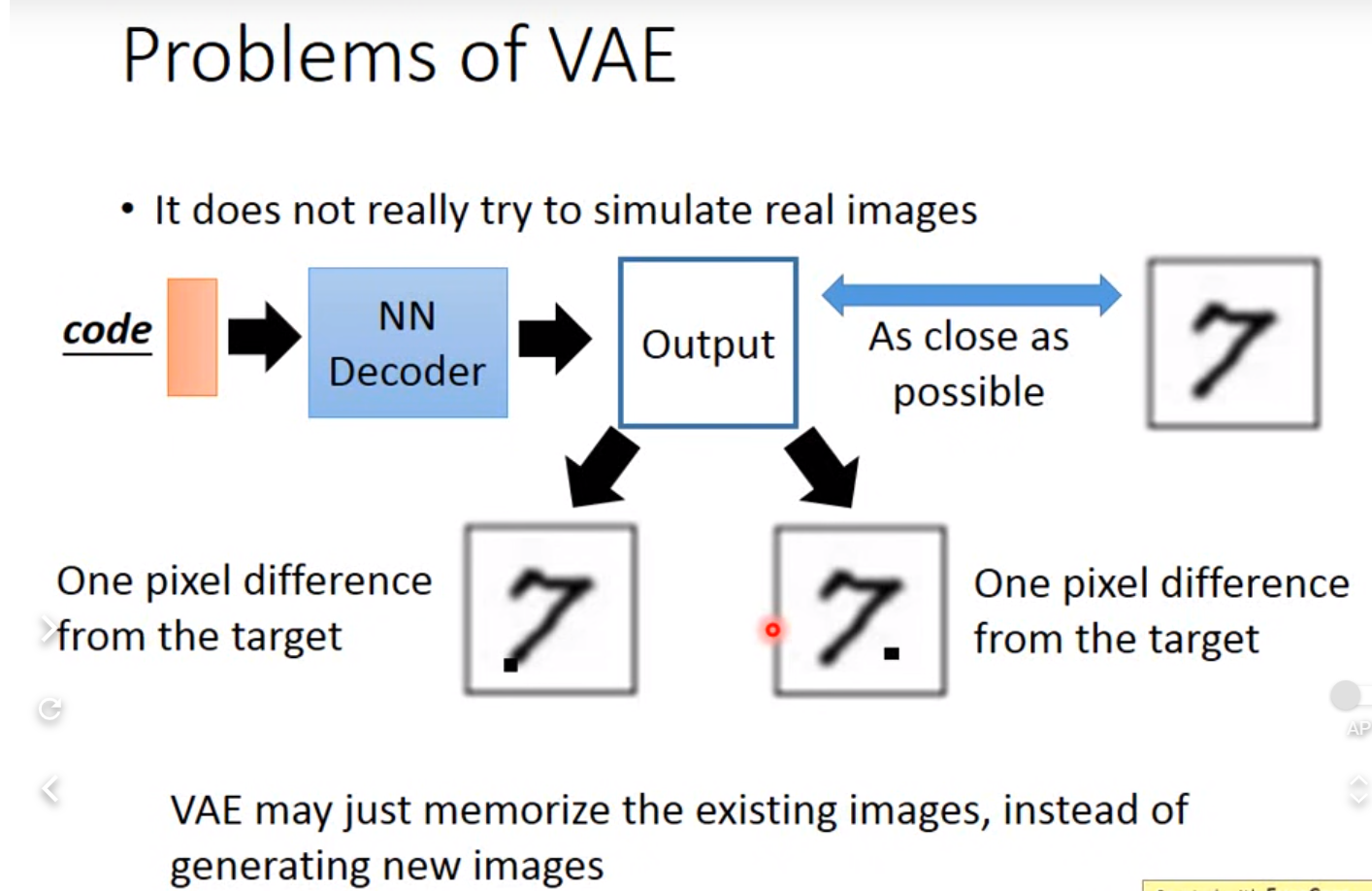 只是想模仿database里面的 没想产生新的
只是想模仿database里面的 没想产生新的
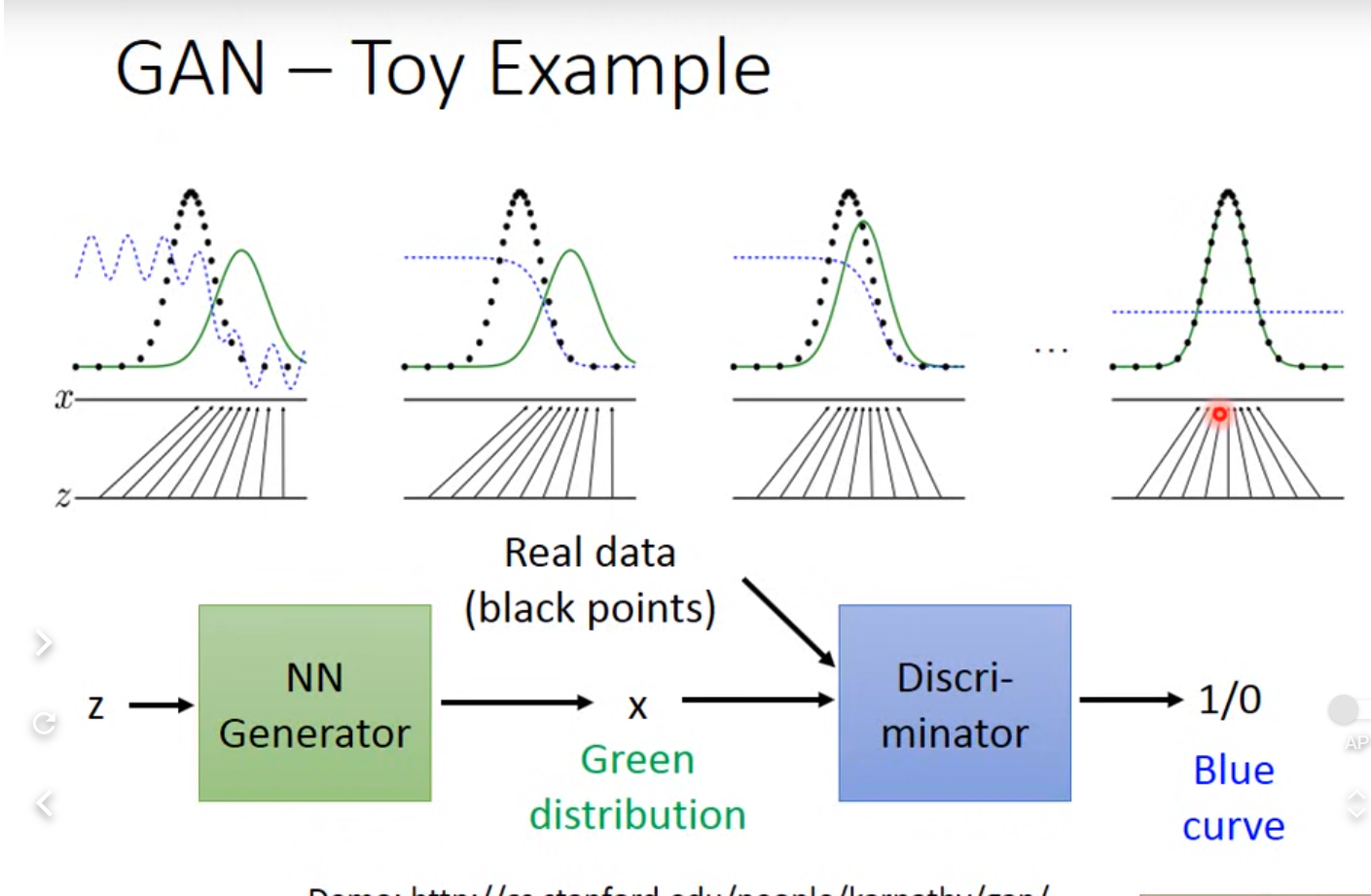
GAN
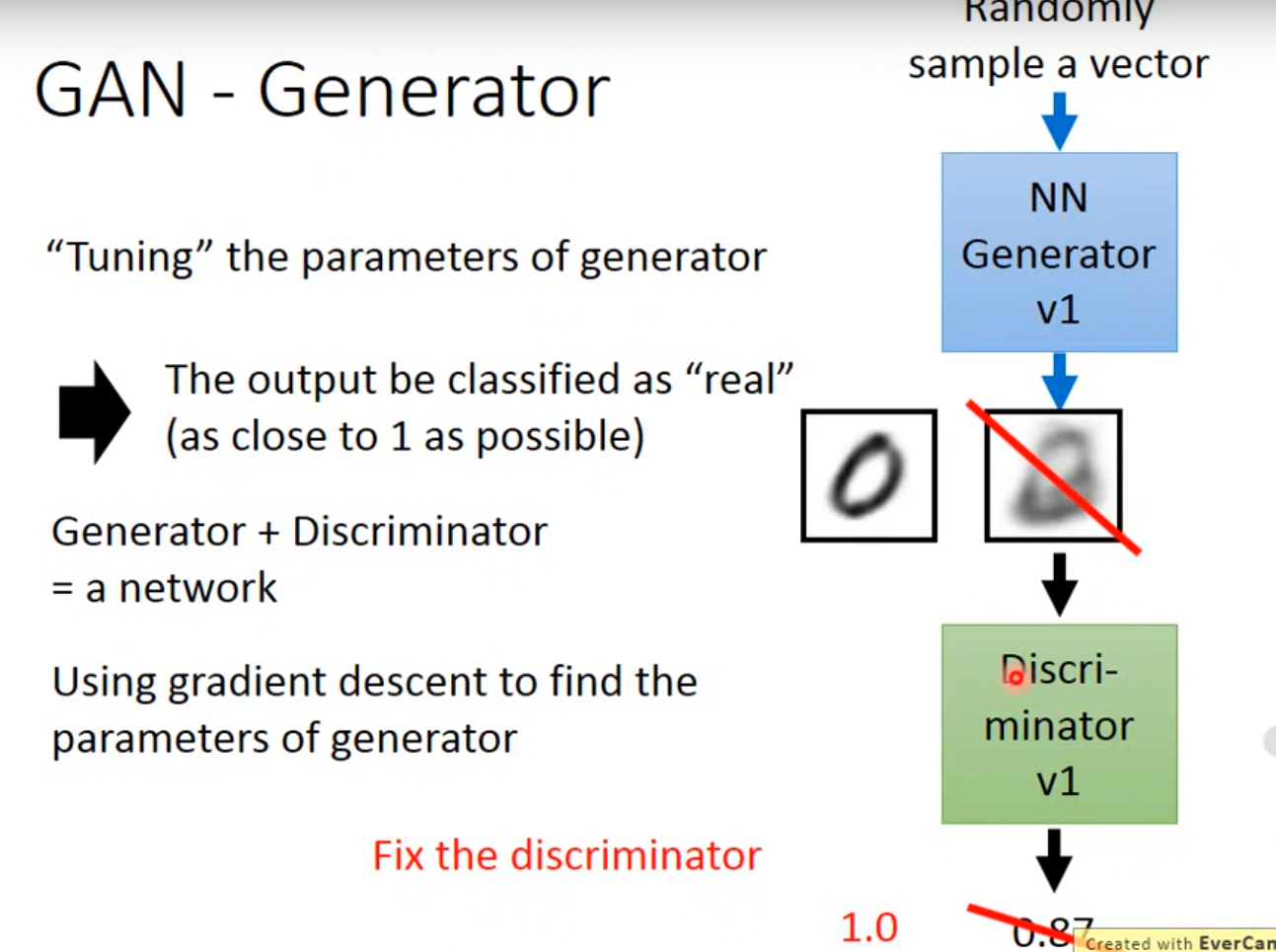
问题:
不知道discriminator是不是对的,如果disc很好 可能是generator 太low
SDE
score-based:
 sde理解
sde理解
-
sde将ddpm 和 score-based 统一一个框架,本质还是估计score
-
sde_based diffusion
-
f(x,t): drift coefficient g(t) : diffusion coeffient w: Brownian motion
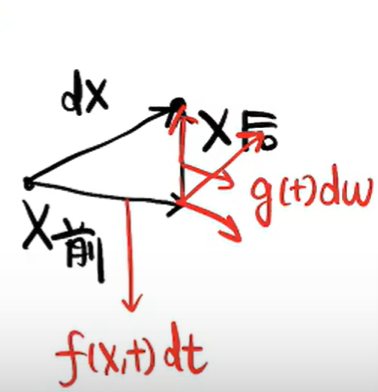
-
重建
- 化log,泰勒一阶展开,是关于t函数,求导会有两项
注;多元函数泰勒:
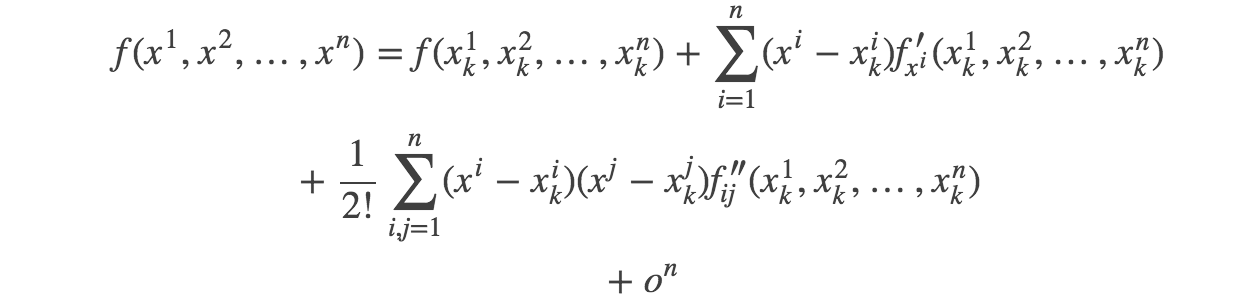
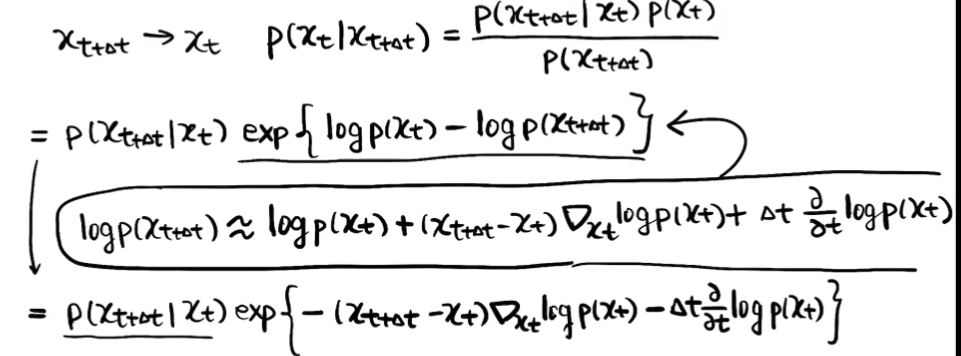

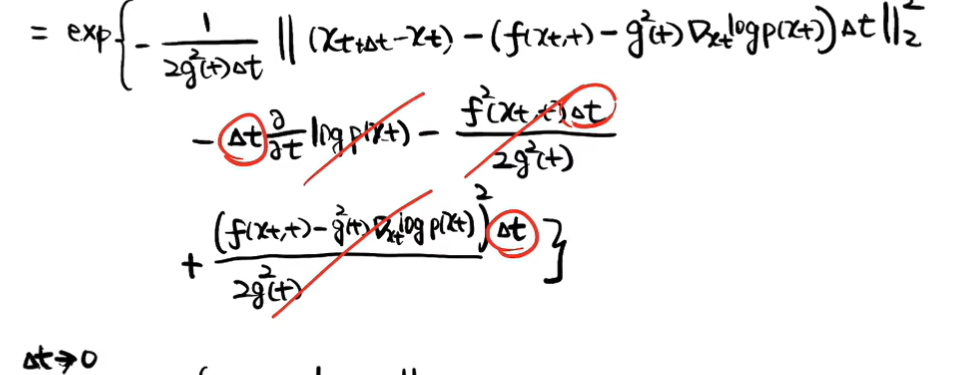

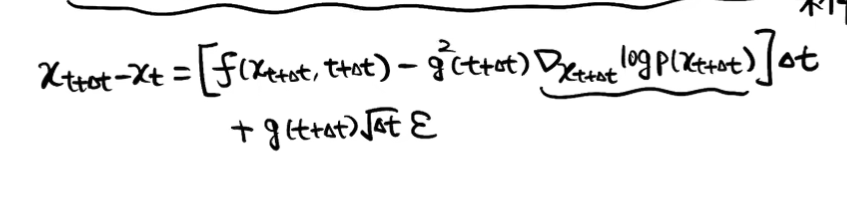 实际上是求score
实际上是求score - 扩散&重建:
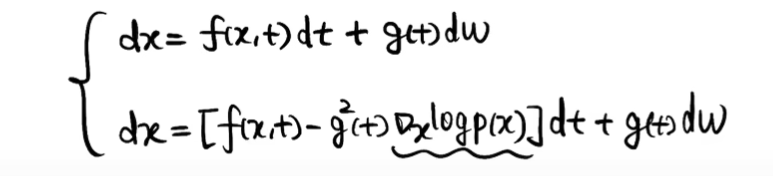
-
-
VE-SDE & VP-SDE
Q&A
- 生成器通过某些“捷径”骗过判别器,导致效果并不好??
-
- 随机流(Stochastic Flow):在数学和统计学中,随机流是指随机变量的序列或过程,它们随时间或某个参数变化。这些流经常用于描述随时间演变的随机系统,例如金融市场中的股价变动、物理系统中的粒子运动等。在机器学习和深度学习中,随机流可以指由随机变量驱动的神经网络的行为或输出。
- VAE
- 通过控制某一dim来控制输出(原来pixelrnn不可以吗
- Diffusion